About Me
I am currently part of the AI Research team at JP Morgan Chase & Co. as Senior Research Associate. I obtained my PhD in Computer Science at the DTAI Lab of the Department of Computer Science of KU Leuven, under the supervision of professor Luc De Raedt. My research was also supervised by professors Jesse Davis and Angelika Kimmig (DTAI Lab).
My main PhD project was Solving Combinatorial and Probabilistic Problems in Natural Language, which aims to build a system capable of understanding and solving probability and combinatorial problems expressed in natural language. Other lines of research included Probabilistic Logic Programming, Knowledge Compilation and Argumentation.
My Bachelor and Master education took place in Udine (Italy), with an Erasmus period of 6 months at the University of Potsdam.
- (Probabilistic) Logic Programming
- Knowledge Representation and Reasoning
- Lifted Inference
- Natural Language Processing
- Argumentation
PhD in Artificial Intelligence
KU Leuven - DTAI lab, Belgium
Erasmus
Potsdam Universität, Germany
MSc Computer Science
Università degli studi di Udine, Italy
BSc Computer Science
Università degli studi di Udine, Italy
Experience
Senior AI Research Scientist
J.P. Morgan & Chase, Spain
Education
PhD in Artificial Intelligence
KU Leuven - DTAI lab, BelgiumRead ThesisDetails of my PhD
- Focus on Declarative Languages and Automated Reasoning.
- Teaching Assistant for the courses:
- Databases (BSc)
- Advanced Programming Languages in AI (MSc)
- Thesis “Declarative Modelling and Reasoning for Combinatorial Problem Solving and Argumentation under Uncertainty”.
Erasmus
Potsdam Universität, GermanyCourses from the Master in Cognitive Systems
- Advanced Problem Solving Techniques
- Argumentation Mining
- Introduction to Deep Learning
- Natural Language Processing
MSc Computer Science
Università degli studi di Udine, ItalyLanguages and Algorithms path
- Advanced Algorithms
- Algorithms and Complexity
- Applied Statistics and Data Analisys
- Advanced Databases
- Automated Reasoning
- Automated System Verification: Theory and Applications
- Models and Algorithms for Decisions
- Network science
BSc Computer Science
Università degli studi di Udine, Italy
Advanced Messaging Platform (AMP): Pipeline for Automated Enterprise Email Processing
Understanding and effectively responding to email communication remains a critical yet complex challenge for current AI techniques, especially in corporate environments. These …
Simerjot Kaur, Charese Smiley, Keshav Ramani, Elena Kochkina, Mathieu Sibue, Samuel Mensah, Pietro Totis, Cecilia Tilli, Toyin Aguda, Daniel Borrajo, Manuela Veloso
Unveiling Interesting Insights: Monte Carlo Tree Search for Knowledge Discovery
Organizations are increasingly focused on leveraging data from their processes to gain insights and drive decision-making. However, converting this data into actionable knowledge …
Pietro Totis, Alberto Pozanco, Daniel Borrajo
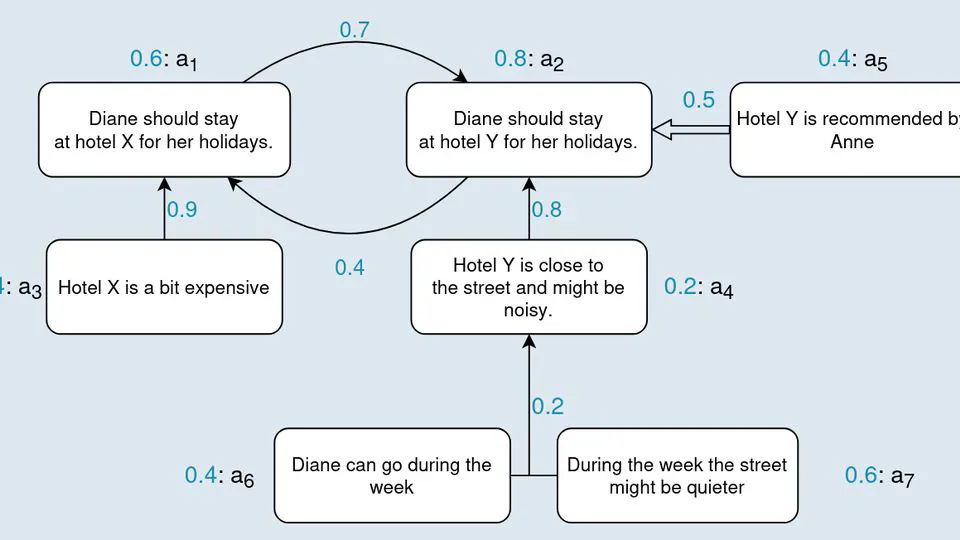
Understanding ProbLog as Probabilistic Argumentation
We show that ProbLog is an instance of a form of Probabilistic Abstract Argumentation (PAA) that builds upon Assumption-Based Argumentation (ABA). The connections pave the way …
Francesca Toni, Nico Potyka, Markus Ulbricht, Pietro Totis
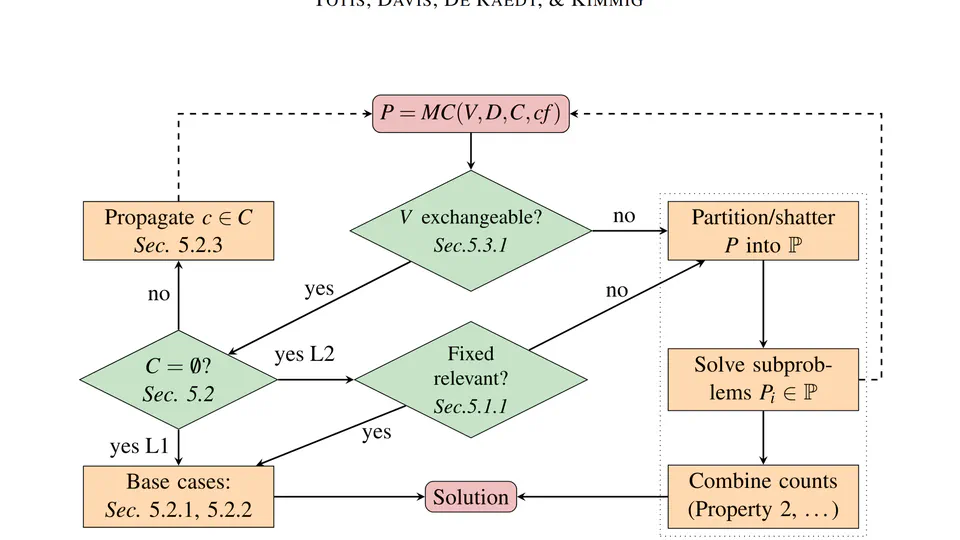
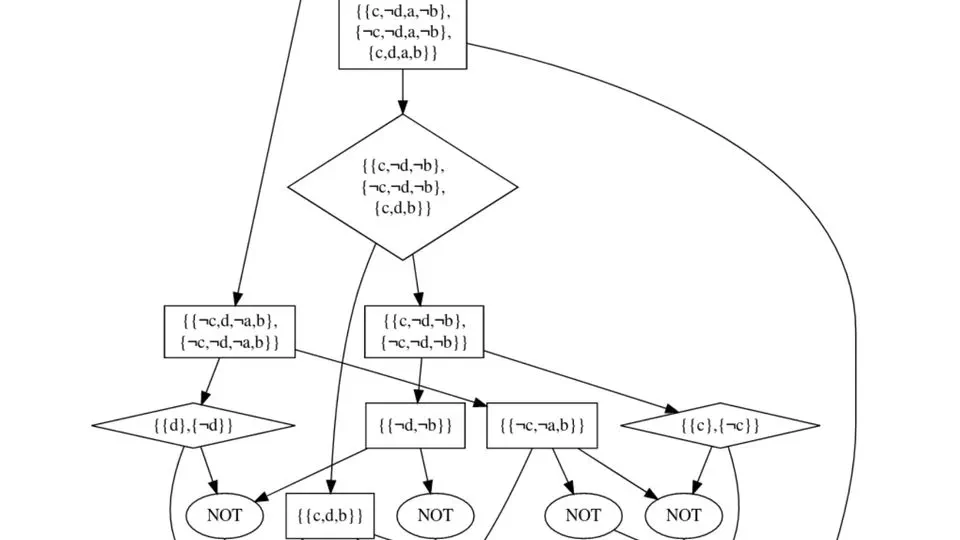
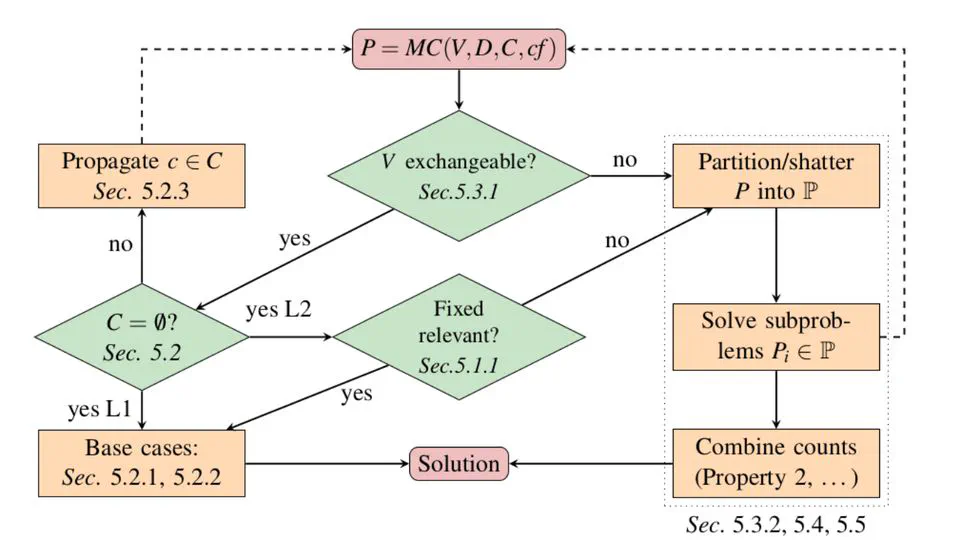
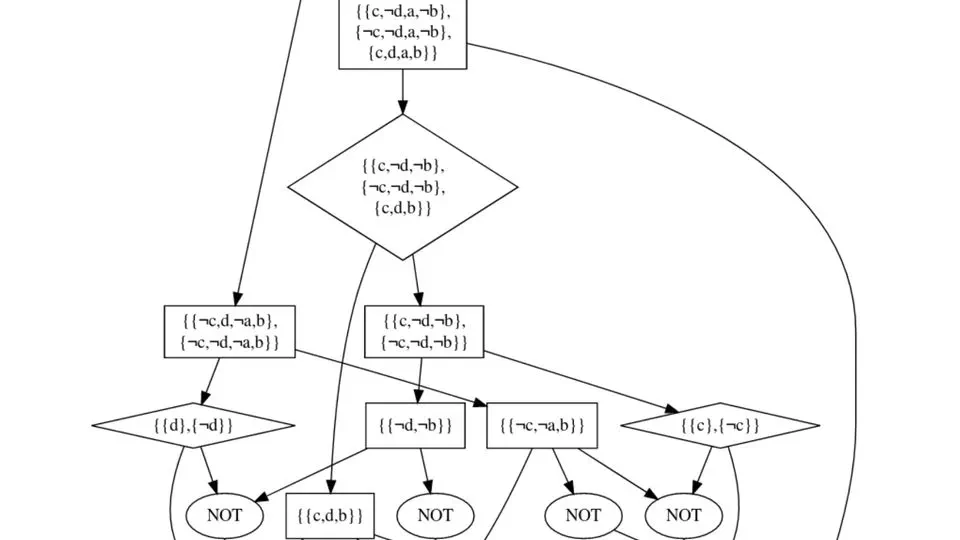
Lifted Reasoning for Combinatorial Counting
In this paper we tackle the problem of automating the resolution of combinatorics math word problems. We introduce CoLa, a novel declarative language to express combinatorics math …
Pietro Totis, Jesse Davis, Luc De Raedt, Angelika Kimmig
Efficient Knowledge Compilation Beyond Weighted Model Counting
We introduce second level algebraic model counting (2AMC) problems, a framework generalizing several probabilistic inference task. We present a novel Knowledge Compilation …
Rafael Kiesel, Pietro Totis, Angelika Kimmig